teoria de colas (modelos de linea de espera )

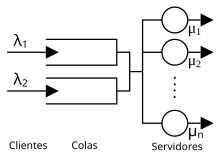
Diagrama que muestra dos colas y múltiples nodos servidores. La teoría de colas estudia los tiempos de espera y capacidad del sistema.

La teoría de colas es el estudio matemático de las colas o líneas de espera dentro de un sistema. Ésta teoría estudia factores como el tiempo de espera medio en las colas o la capacidad de trabajo del sistema sin que llegue a colapsarse. Dentro de las matemáticas, la teoría de colas se engloba en la investigación de operaciones y es un complemento muy importante a la teoría de sistemas y la teoría de control. Se trata así de una teoría que encuentra aplicación en una amplia variedad de situaciones como negocios, comercio, industria, ingenierías, transporte y logística o telecomunicaciones.

Los modelos de línea de espera consisten en fórmulas y relaciones matemáticas que pueden usarse para determinar las características operativas (medidas de desempeño) para una cola. 
Las características operativas de interés incluyen las siguientes:
Probabilidad de que no haya unidades o clientes en el sistema
Cantidad promedio de unidades en la línea de espera
Cantidad promedio de unidades en el sistema (la cantidad de unidades en la línea de espera más la cantidad de unidades que se están atendiendo)
Tiempo promedio que pasa una unidad en la línea de espera
Tiempo promedio que pasa una unidad en el sistema (el tiempo de espera más el tiempo de servicio)
Probabilidad que tiene una unidad que llega de esperar por el servicio.

Los gerentes que tienen dicha información son más capaces de tomar decisiones que equilibren los niveles de servicio deseables con el costo de proporcionar dicho servicio.

DISTRIBUCIÓN DE LLEGADAS

Para determinar la distribución de probabilidad para la cantidad de llegadas en un período dado, se puede utilizar la distribución de Poisson. /= Media o cantidad promedio de ocurrencia en un intervalo e= 2.17828 X= cantidad de ocurrencias en el intervalo

DISTRIBUCIÓN DE TIEMPO DE SERVICIO

El tiempo de servicio es el tiempo que pasa un cliente en la instalación una vez el servicio ha iniciado. Se puede utilizar la distribución de probabilidad exponencial para encontrar la probabilidad de que el tiempo de servicio sea menor o igual que un tiempo t. e= 2.17828 μ= cantidad media de unidades que pueden servirse por período

DISCIPLINA DE LA LINEA DE ESPERA

Manera en la que las unidades que esperan el servicio se ordenan para recibirlo. El primero que llega, primero al que se le sirve Último en entrar, primero en salir Atención primero a la prioridad más alta

OPERACIÓN DE ESTADO ESTABLE

Generalmente la actividad se incrementa gradualmente hasta un estado normal o estable. El período de comienzo o principio se conoce como período transitorio, mismo que termina cuando el sistema alcanza la operación de estado estable o normal.

MODELOS DE LÍNEA DE ESPERA DE UN SOLO CANAL CON LLEGADAS DE POISSON Y TIEMPOS DE SERVICIO EXPONENCIALES

A continuación, las fórmulas que pueden usarse para determinar las características operativas de estado estable para una línea de espera de un solo canal. El objetivo de las fórmulas es mostrar cómo se puede dar información acerca de las características operativas de la línea de espera.

¿COMO SE PUEDE MEJORAR LA OPERACION DE LINEA DE ESPERA?

Características operativas para el sistema con la tasa media de servicio aumentada a μ=1.25 clientes por minuto.

Las limitaciones del acercamiento matemático

La teoría de formación de una cola es a menudo demasiado restrictiva matemáticamente para ser capaz de modelar todas las situaciones verdaderas a nivel mundial. Por ejemplo; los modelos matemáticos a menudo asumen el número de clientes, o la capacidad de la cola infinitos, cuando es evidente que deben estar limitados. Los medios alternativos del análisis de la teoría de colas consisten generalmente en simulaciones de ordenador y/o en el análisis de datos experimentales.
Aplicación a la telefonía

Las redes telefónicas se diseñan para acomodar la intensidad ofrecida del tráfico con solamente una pequeña pérdida. El funcionamiento de los sistemas depende de si la llamada es rechazada, de si está perdida, etc. Normalmente los sistemas de desbordamiento hacen uso de rutas alternativas e incluso estos sistemas tienen una capacidad de carga finita o máxima de tráfico. Sin embargo, el uso de las colas permite que los sistemas esperen por las peticiones de su cliente hasta que los recursos libres estén disponibles. Esto significa que si los niveles de la intensidad del tráfico exceden de la capacidad disponible, las llamadas del cliente se perderían. La disciplina de colas determina la manera de cómo manejar las llamadas de los clientes. Define la manera en que les servirán, la orden de las cuales se sirven, y la manera en la que los recursos se dividen entre los 

clientes.http://metodoscuantitativo2.galeon.com/enlaces2219625.html